Pengertian aritmatika

argumiwangAji Gumiwang
3 
Sep '17
Aritmatika
Aritmatika dari kata bahasa Yunani arithnos = angka atau dulu disebut ilmu hitung merupakan cabang (atau pendahulu) matematika yang mempelajari operasi dasar bilangan. Oleh orang awam, kata “aritmetika” sering dianggap sebagai sinonim dari teori bilangan.
Apakah yang dimaksud dengan Aritmetika ?
dlschnsDelischa Novia Sabilla
1 
Sep '17
  1. BARIS ARITMATIKA
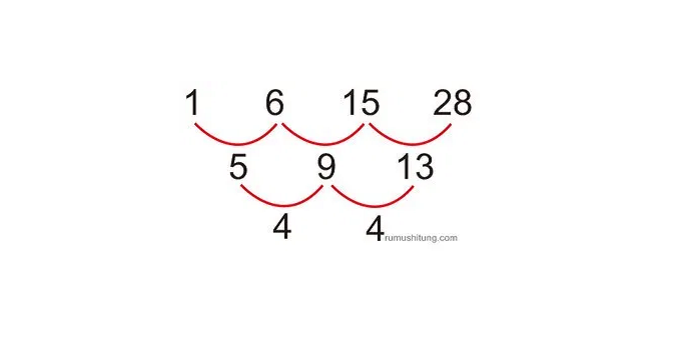
Pertama dimulai dari barisan, barisan bilangan adalah urutan dari bilangan yang dibuat berdasarkan aturan tertentu. Sedangkan untuk barisan aritmatika adalah sebuah barisan bilangan dimana setiap pasangan suku-suku yang berurutan memiliki selisih yang sama.
contoh : 6,9,12,15,…
Selisih bilangan pada barisan aritmatika disebut beda yang biasa disimbolkan dengan huruf b, untuk contoh diatas memiliki nilai beda 3. Dan bilangan yang menyusun suatu barisan disebut suku, dimana suku ke n dari suatu barisan disimbolkan dengan Un sehingga untuk suku ke 5 dari suatu barisan biasa disebut dengan U5. Khusus untuk suku pertama dari suatu barisan biasa disimbolkan dengan huruf a.
Jadi bentuk umum untuk suatu barisan aritmatika yaitu:
U1,U2,U3, … ,Un-1 atau a, a+b, a+2b, … , a+(n-1)b
Menentukan Rumus Suku ke-n suatu barisan
Pasangan suku-suku berurutan dari suatu barisan aritmatika mempunyai beda yang sama, maka
U2 = a + b
U3 = U2 + b = (a + b) + b = a + 2b
U4 = U3 + b = (a + 2b) + b = a + 3b
U5 = U4 + b = (a + 3b) + b = a + 4b
Berdasarkan pola tersebut, dapatkah sobat menentukan suku ke-7, suku ke-26 hingga suku ke-90? Dengan menggunakan pola diatas kita dapat mengetahui dengan mudah suku-suku tersebut.
U7 = a + 6b
U26 = a + 25b
U90 = a + 89b
Sehingga berdasarkan runtutan penjelasan diatas, dengan menyambungkannya dengan proses generalisasi sebagai karakteristik dari computational thinking, untuk suku ke-n dapat kita peroleh menggunakan rumus :
Un = a + (n – 1)b, untuk n bilangan asli
proses tersebut merupakan generalisasi computational thinking yaitu mengadaptasi suatu permasalahan yang telah terpecahkan untuk membuat suatu solusi terhadap masalah yang serupa, sehingga ditemukannya rumus baris aritmatika.
  1. DERET ARITMATIKA
Yang dimaksud dengan deret aritmatika adalah penjumlahan dari semua anggota barisan aritmatika secara berurutan. Contoh dari deret aritmatika yaitu:
7 + 10 + 13 + 16 + 19 + …
Misalnya kita ambil n suku pertama, jika kita ingin menentukan hasil dari deret aritmatika sebagai contoh untuk 5 suku pertama dari contoh deret diatas. Bagaimana caranya?
7 + 10 + 13 + 16 + 19 = 65
Nah untuk 5 suku pertama, masih mungkin kita menghitung manual seperti diatas. Seandainya kita akan menentukan jumlah dari 100 suku pertama, apakah masih mungkin kita menghitung manual seperti itu. Walaupun bisa tetapi pastinya akan memakan waktu yang cukup lama. Sebagai contohnya untuk mennetukan jumlah 5 suku pertama dari contoh diatas.
Misalkan S5=7 + 10 + 13 + 16 + 19, sehingga
S5 = 7 + 10 + 13 + 16 + 19
S5 = 19 + 16 + 13 + 10 + 7
-----------------------------------------+
2S5 = 26 + 26 + 26 + 26 + 26
Walaupun dengan cara yang berbeda tetapi menunjukkan hasil yang sama yaitu 65. Perhatikan bahwa S5 tersebut dapat dicari dengan mengalikan hasil penjumlahan suku pertama dan suku ke-5, dengan banyaknya suku pada barisan, kemudian dibagi dengan 2. Analogi dengan hasil ini, dengan proses generalisasi computational thinking, jumlah n suku pertama dari suatu barisan dapat dicari dengan rumus berikut:
Sn = (a + Un) × n : 2
Dikarenakan Un = a + (n – 1)b, sehingga rumus di atas menjadi:
Sn = (2a + (n – 1)b) × n : 2
mazizkMuhammad Aziz Kusworo
2 
Sep '17
Pengertian Aritmetika dan Fungsinya
Aritmatika adalah cabang matematika yang bersangkutan dengan penambahan, pengurangan, perkalian, pembagian, dan ekstraksi akar nomor-nomor tertentu yang dikenal sebagai bilangan real.
Aritmatika juga dapat ilmu hitung dasar yang merupakan bagian dari matematika. Operasi dasar aritmatika adalah penjumlahan, pengurangan, perkalian dan pembagian, Walaupun operasi-operasi lain yang lebih canggih (seperti persentase, akar kuadrat, pemangkatan, dan logaritma) kadang juga dimasukkan ke dalam kategori ini.
Perhitungan dalam aritmatika dilakukan menurut suatu urutan operasi yang menentukan operasi aritmatika yang mana lebih dulu dilakukan.
  1. Penjumlahan (+) adalah salah satu operasi aritmatika dasar. Penjumlahan merupakan penambahan dua bilangan menjadi suatu bilangan yang merupakan Jumlah. Penambahan lebih dari dua bilangan dapat dipandang sebagai operasi Penambahan berulang, prosedur ini dikenal sebagai Penjumlahan Total (summation), yang mencakup juga penambahan dari barisan bilangan tak hingga banyaknya (infinite).
  2. Pengurangan (-) adalah lawan dari operasi penjumlahan. Pengurangan mencari ‘perbedaan’ antara dua bilangan A dan B (A-B), hasilnya adalah Selisih dari dua bilangan A dan B tersebut. Bila Selisih bernilai positif maka nilai A lebih besar daripada B, bila Selisih sama dengan nol maka nilai A sama dengan nilai B dan terakhir bila Selisih bernilai negatif maka nilai A lebih kecil daripada nilai B.
  3. Perkalian (*) pada intinya adalah penjumlahan yang berulang-ulang. Perkalian dua bilangan menghasilkan Hasil Kali (product), sebagai contoh 4*3 = 4+4+4 = 12.
  4. Pembagian (/) adalah lawan dari perkalian. Pembagian dua bilangan A dan B (A/B) akan menghasilkan Hasil Bagi (quotient). Sembarang pembagian dengan bilangan nol (0) tidak didefinisikan. Selanjutnya bila nilai Hasil Bagi lebih dari satu, berarti nilai A lebih besar daripada nilai B, bilai Hasil Bagi sama dengan satu, maka berarti nilai A sama dengan nilai B, dan terakhir bila Hasil Baginya kurang dari satu maka nilai A kurang dari nilai B.
Aritmatika yang dipelajari untuk anak Sekolah Dasar berupa bilangan yang berkisar antara bilangan puluhan, ratusan, dan ribuan. Anak Sekolah Dasar dalam mempelajarinya berdasarkan tingkatan kelas yang ditempuh, untuk kelas 1 Sekolah Dasar hanya berkisar bilangan puluhan, untuk anak kelas 2 sampai bilangan ratusan, dan untuk anak kelas 3 sampai bilangan ribuan.
Melalui belajar mental aritmatika seorang anak akan memperoleh banyak manfaat diantaranya :
  1. Meningkatkan kemampuan berhitung lebih cepat diatas rata-rata anak.
  2. Kemampuan mencongak lebih cepat dan tepat.
  3. Menyeimbangkan penggunaan otak kiri dan kanan serta mengoptimalkannya untuk mencapai tingkat berfikir yang analisis dan logika berfikir yang benar.
  4. Terlatihnya daya fikir dan konsentrasi, membantu anak untuk menguasi mata pelajaran yang lainnya.
  5. Menumbuhkembangkan imajinasi sehingga kreatifitas anak berkembang.
  6. Membiasakan diri dengan angka-angka, membuat anak tidak lagi alergi pada pelajaran eksakta.
sumber:

2 BULAN KEMUDIAN
Oktavya_Ningtiyas
1d
image
Aritmatika atau aritmetika merupakan bagian dari matematika yang mempelajari tentang operasi dasar bilangan (penjumlahan, pengurangan, perkalian dan pembagian). Berawal dari memahami serta menguasai operasi dasar dan pemikiran yang sederhana tersebut, siswa akan mampu meningkatkan kemampuannya untuk mempelajari cabang matematika pada tingkatan yang lebih rumit (Nursuprianah & Nisa, 2013). Aritmatika terdapat 2 macam yaitu barisan aritmatika dan deter aritmatika.
  1. Barisan Aritmatika
    Barisan aritmatika sering juga disebut barisan hitung adalah barisan bilangan
    yang setiap sukunya diperoleh dari suku sebelumnya dengan menambah atau
    mengurangi dengan suatu bilangan tetap. Bilangan tetap tersebut dinamakan
    pembeda, (biasanya disimbolkan dengan b). Jadi pembeda merupakan selisih antara dua suku yang berturutan. Suku pertama barisan aritmetika ditulis U1 , sedangkan suku ke-n dari suatu barisan bilangan aritmatika dituliskan sebagai Un.
    • Rumus suku ke-n dari barisan aritmatika
      Untuk menentukan suku ke-n suatu barisan bilangan aritmetika dimana n relatif besar tentunya akan sulit jika kita harus menuliskan seluruh anggota barisan bilangan tersebut. Untuk itu diperlukan cara untuk menentukan suku ke-n dari suatu barisan bilangan aritmetika dengan n sembarang bilangan asli. Misal suku pertama suatu barisan aritmetika adalah a dengan pembeda b, maka barisan aritmetika tersebut dapat dituliskan sebagai berikut :
      a, a + b, a + b + b, a + b + b + b, ….
      atau dapat dituliskan
      a, a + b, a + 2b , a + 3b, …
      Sehingga dapat dibuat tabel berikut:
      image
      Jadi rumus suku ke-n dari barisan aritmetika adalah: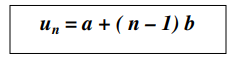
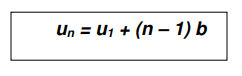
      image atau image
      image
      Barisan aritmatika yang bilangan-bilangannya semakin besar nilainya disebut barisan aritmatika naik, sedangkan barisan aritmatika yang bilangan-bilangannya semakin kecil nilainya disebut barisan aritmatika turunn. Pembeda pada barisan aritmatika naik bernilai positif, sedangkan pembeda pada barisan aritmatika turun adalah negatif.
    • Rumus Suku Tengah Barisan Aritmetika
      Pada barisan aritmetika, suku yang terletak di tengah jika banyaknya suku ganjil dinamakan suku tengah. Misalnya diberikan barisan aritmetika U1, U2, U3, … Un
      dengan n ganjil dan suku tengahnya adalah Ut maka berlaku :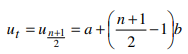
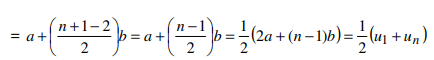
      image image
      Jadi suku tengah barisan aritmetika adalah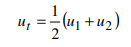
      image
    • Suku sisipan
      Misalkan diberikan dua bilangan p dan q, kemudian disisipkan k buah bilangan diantara kedua bilangan tersebut sehingga membentuk barisan aritmetika dengan beda b sebagai berikut:
      p, (p + b), (p +2b), …, (p+kb), q
      maka beda b dari barisan tersebut dapat ditentukan sebagai berikut: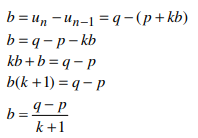
      image
      Jadi beda barisan aritmetika yang terbentuk adalah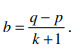
      image
  2. Deret Aritmatika
    Perhatikan barisan aritmetika 3, 5, 7, 9, …
    Dari barisan aritmetika tersebut dapat dibuat suatu deret aritmetika :
    Sn = 3 + 5 + 7 + 9 +…
    Dengan demikian jika diketahui suatu barisan bilangan aritmetika : U1, U2, U3, … Un
    maka dapat dibuat suatu deret aritmetika:
    Sn = U1 + U2 + U3 +…+ Un
    Bentuk umum rumus Sn yaitu :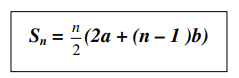
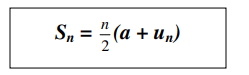
    image atau image
    Untuk setiap deret aritmetika berlaku :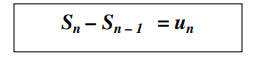
    image
    dimana (Un = suku ke n dari deret aritmetika)

Komentar

Posting Komentar

Postingan populer dari blog ini

Geguritan

Di mading sekolah ataupun di media sosial sering kali kita melihat sebuah puisi dengan bahasa jawa yang memiliki arti tertentu dan ada banyak tema yang dipakai. Biasanya kata-kata yang digunakan dalam geguritan menggunakan kata yang sedikit asing bagi kamu yang tidak pandai bahasa jawa dan memiliki makna tertentu di dalamnya. Meskipun kamu sering melihat puisi dalam bentuk bahasa jawa atau geguritan tersebut, namun apakah kamu tahu pengertian dari Geguritan. Daftar Isi  [ show ] Pengertian Geguritan Pengertian dari Geguritan adalah sebuah karya sastra jawa yang cara pembuatannya menggunakan kalimat yang indah dan mempunyai makna. Cara pengungkapan Geguritan ini menggunakan bahasa yang mempunyai rima, irama, mitra, baik serta penyusunan yang tepat. Selain itu, geguritan juga bisa dibuat berdasarkan ungkapan persaan dan pikiran. Dalam bahasa Indonesia, geguritan disebut dengan puisi. Sebenarnya geguritan dan puisi hampir sama, yang membedakan hanya bahasa yang digunaka
Baca selengkapnya

Keutamaan haji

Gambar
      Belajar Islam Hukum Islam Faedah Ilmu Naskah Khutbah Ebook Video Kajian About Me Home     Haji Umrah     6 Keutamaan Ibadah Haji HUKUM ISLAM HAJI UMRAH 6 Keutamaan Ibadah Haji By   Muhammad Abduh Tuasikal, MSc  -   October 22, 2011   13012   0 Sudah kita ketahui bersama bahwa haji adalah ibadah yang amat mulia. Ibadah tersebut adalah bagian dari rukun Islam bagi orang yang mampu menunaikannya. Keutamaan haji banyak disebutkan dalam Al Qur’an dan As Sunnah. Berikut beberapa di antaranya: Pertama: Haji merupakan amalan yang paling afdhol. Dari Abu Hurairah  radhiyallahu ‘anhu , ia berkata, سُئِلَ النَّبِىُّ – صلى الله عليه وسلم – أَىُّ الأَعْمَالِ أَفْضَلُ قَالَ « إِيمَانٌ بِاللَّهِ وَرَسُولِهِ » . قِيلَ ثُمَّ مَاذَا قَالَ « جِهَادٌ فِى سَبِيلِ اللَّهِ » . قِيلَ ثُمَّ مَاذَا قَالَ « حَجٌّ مَبْرُورٌ
Baca selengkapnya